Método de integración por partes
Funciones e Integrales Indefinidas
| Función | Integral Indefinida |
|---|---|
| Fórmulas integración por partes | |
| Sea f(x) = uⅆv | Entonces ∫f(x)ⅆx = u*v-∫vⅆu, donde v = ∫ⅆv y ⅆu = u' |
| Fórmulas de sustitución | |
| Sea u = f(x) | Entonces du = f'(x)dx |
| Fórmulas de sustitución trigonométrica | |
| √(a^2 - x^2) | (a^2 * arcsin(x/a) + x√(a^2 - x^2))/2 |
| √(a^2 + x^2) | (x√(a^2 - x^2) + a^2 * ln|(√(a^2 + x^2) + x)/a|)/2 |
| Fórmula para fracciones parciales | |
| Sea f(x) = g(x)/h(x), donde h(x) se puede descomponer usando factorización | Entonces f(x) = A/h0(x) + B/h1(x) + ... |
Diagramas de flujo de los distintos métodos de integración vistos en clase
Método de sustitución
Método sustitución trigonométrica
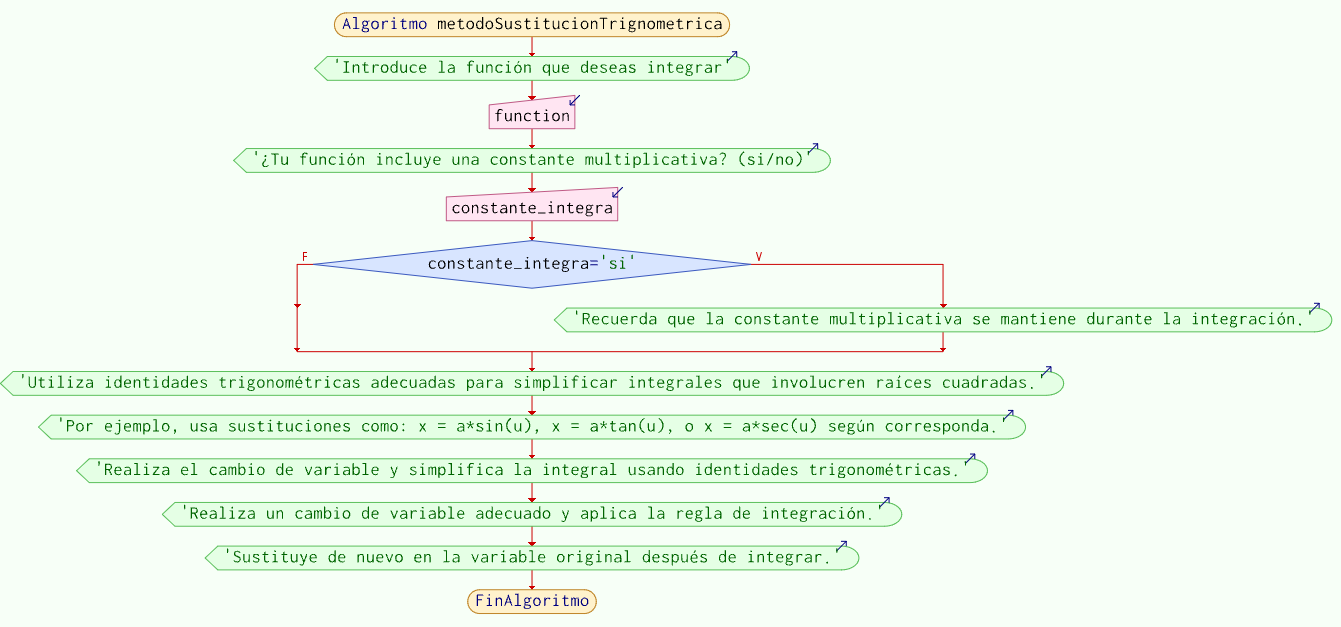
Método de fracciones parciales
Ejercicios resueltos de los diferentes métodos de integración vistos en clase
Calculadora de integrales
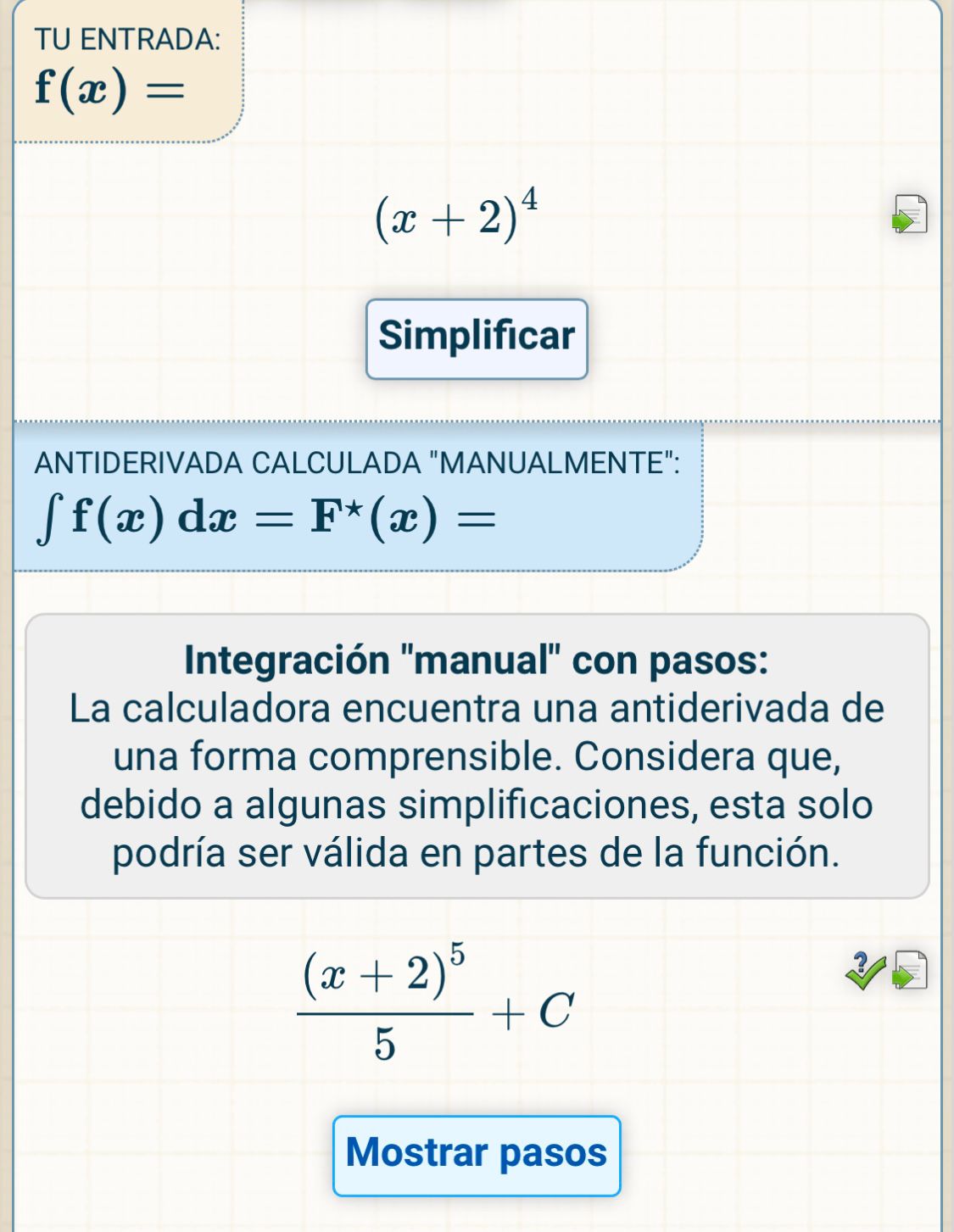
Ejercicio de sustitución
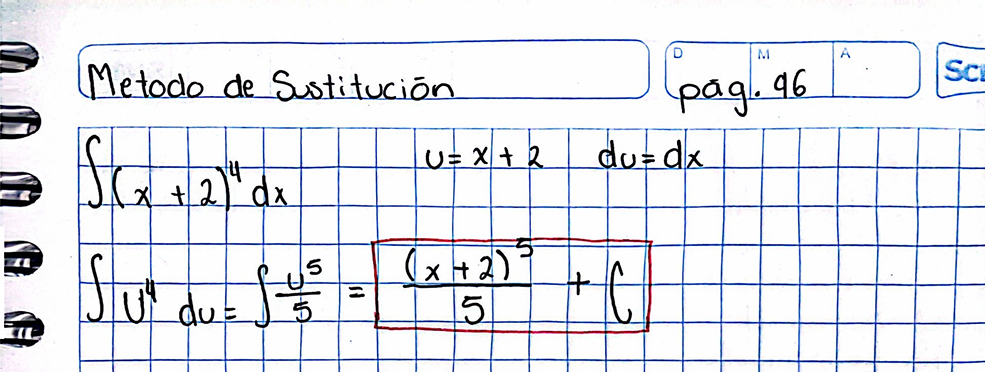
SnapXam
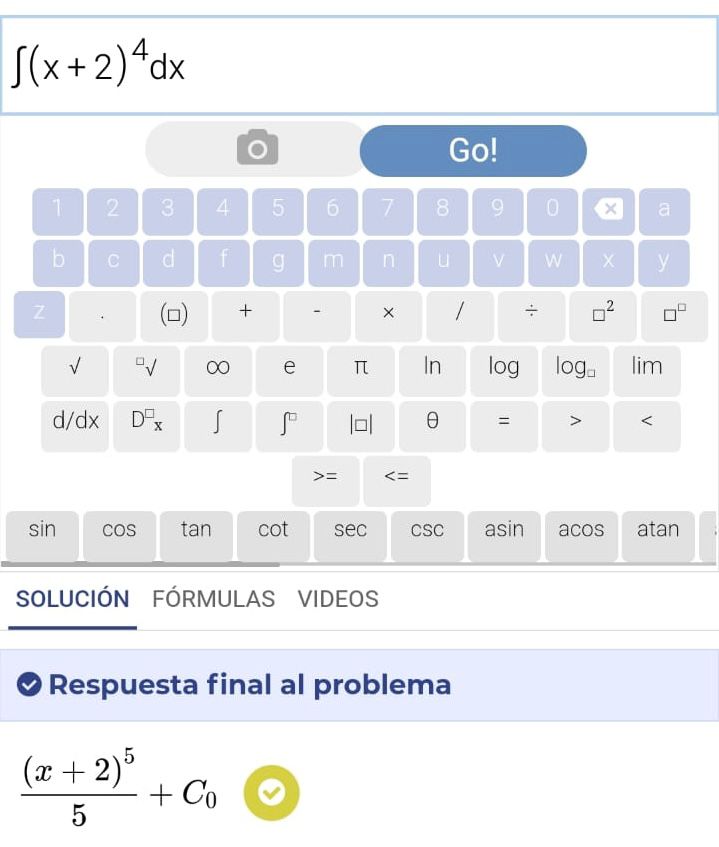
Calculadora de integrales
Ejercicio de integración por partes
GeoGebra
SymboLab
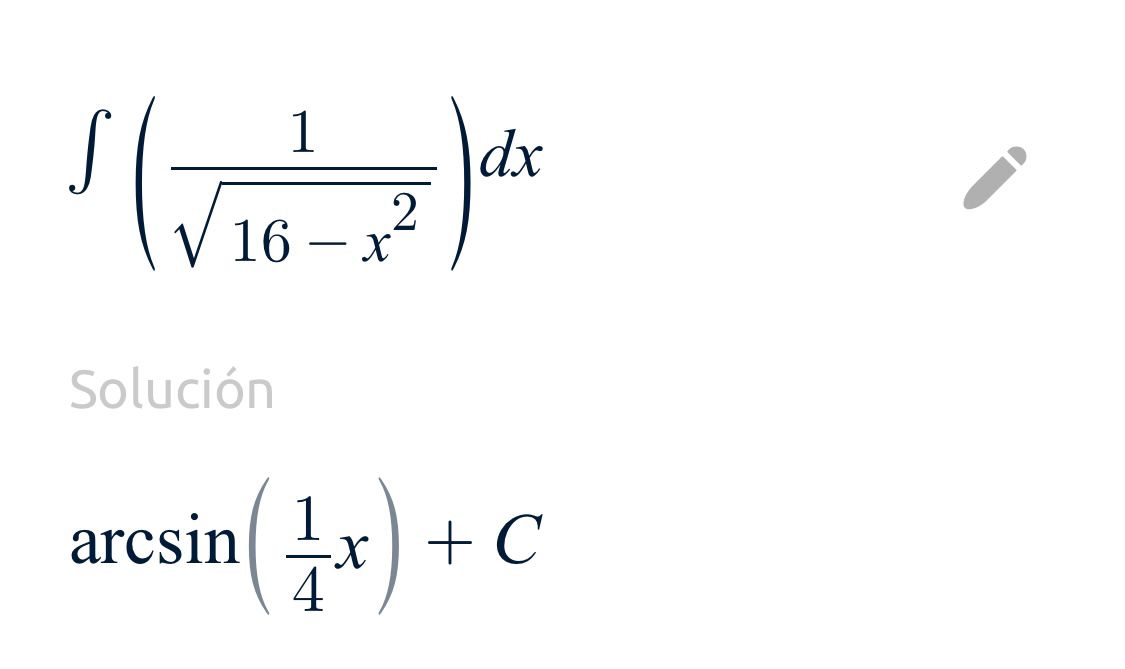
Ejercicio de sustitución trigonométrica
GeoGebra
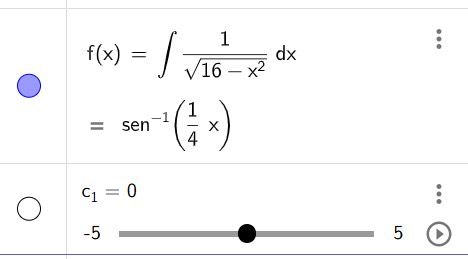
SymboLab
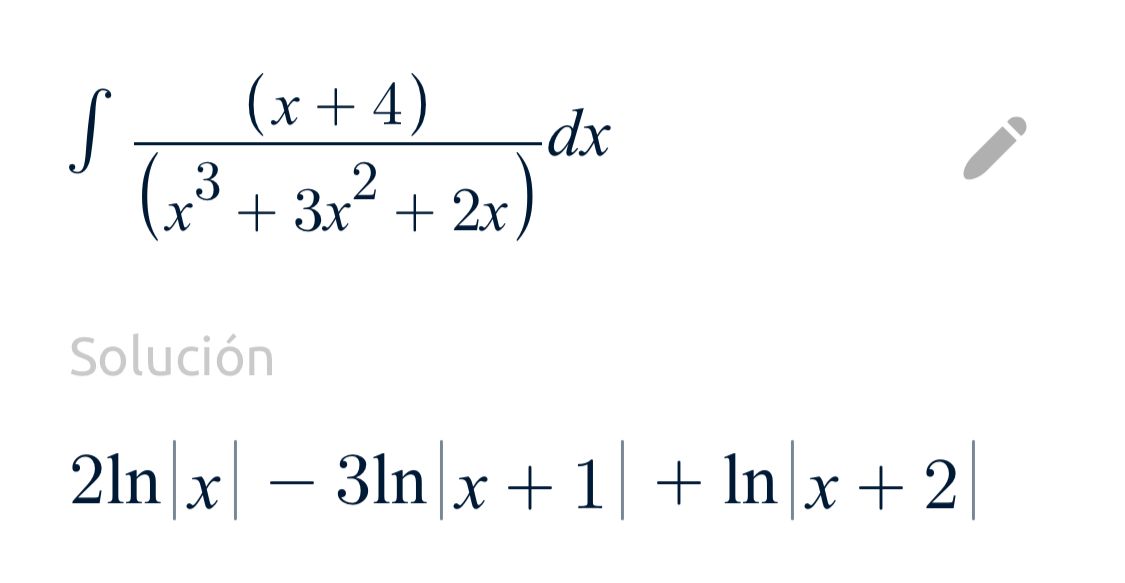
Ejercicio de fracciones parciales
SnapXam
Calculadoras usadas en este proyecto
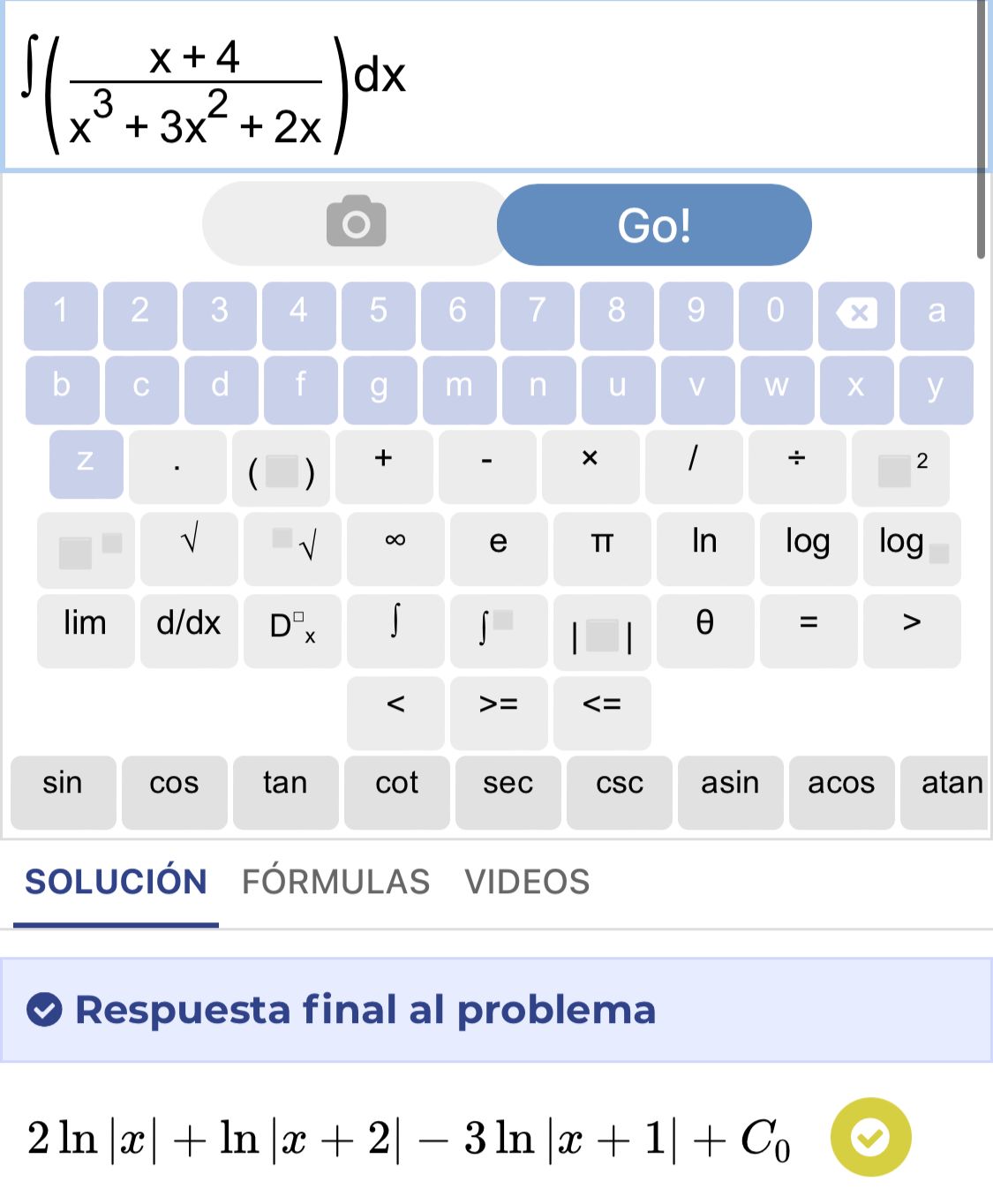
Video de los integrantes